The progressive demand that math education be revised to promote the DEI agenda raises fundamental questions about the nature of mathematics, its relationship to society, and its role in education and life.

We already understand that the relationship between math and society is the consequence flowing from the relationship between math and science, on the one hand, and the well-known relationship between science and society, on the other hand. However, those are conclusions. We need to think about how we got there.

What is the relationship between math and science?

In his introduction to Human Diversity: The Biology of Gender, Race, and Class, Charles Murray explains,

The sciences form a hierarchy. “Physics rests on mathematics, chemistry on physics, biology on chemistry, and, in principle, the social sciences on biology,” wrote evolutionary biologist Robert Trivers.

This places mathematics at the foundation of all the sciences. Galileo Galilei (1564-1642), the father of modern science, was an Italian mathematician, physicist, astronomer, and natural philosopher. Frequently attributed to Galileo is the quip that “Mathematics is the language of science.”

Image by bimbimkha.

That quip is without question a true assertion, and it raises several follow-up questions, two of which are:

(1) If math is the language of science, then what is the language of mathematics?

(2) Exactly what is mathematics?

Each of these two questions has a simple but, perhaps, surprising answer.

First, The language of mathematics is ordinary modern language; that is, English, Spanish, German, Chinese, etc. This means that all that so many math-phobic people view as mathematical gobbledygook is, in reality, a compact and economical rendition of ordinary language.

For a simple example of this, the English statement “Five plus three times some real number x is twenty-three” can be rendered in math-talk as “3x+5=23”. This compact algebraic symbolism is a great convenience, facilitating the development of simple techniques for “solving the equation” that are easily within the grasp of the middle schooler.

As a more complicated example of this, consider the mathematical symbolic statement:

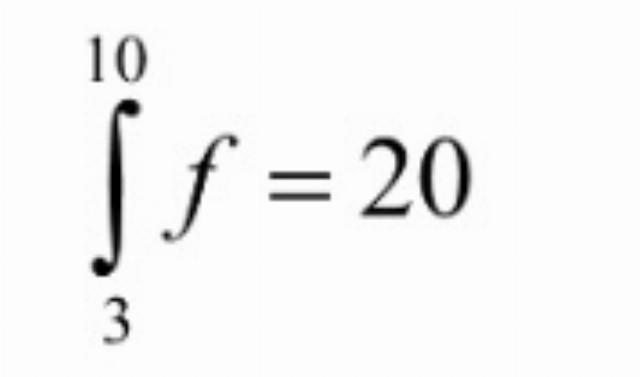
This is the agreed symbolism for the following statement in ordinary English:

For every positive real number epsilon there is a positive real number delta such that for every chain C from 3 to 10 with mesh less than delta and every interpolating sequence I of C, the sum formed by f, C and I is within epsilon of 20.

The average reader unfamiliar with calculus is not expected to understand that passage, but the point is that the English passage and the mathematical notation have the same meaning—and one could do the same with the mathematical notation and any other language.

And secondly, exactly what is mathematics? The answer is simple, albeit perhaps a bit mysterious: Mathematics is logic applied to a quantitative axiom system.

As mathematics is a branch of logic, it serves as a conduit for applying logic to problems. Approaching a problem mathematically is a technique for bringing logic to bear upon it.

Mathematics thus consists of only three kinds of entities: axioms, definitions, and theorems. Theorems are propositions logically deduced from the axioms and definitions.

An axiom is a proposition taken as true without proof. The axiom systems are usually (but not necessarily) deemed (assumed, believed) to describe nature, and the application of logic to the axiom is, therefore, deemed to reveal information about nature.

The key point here is that mathematics, at its essence, is logic applied to nature.

This point is subtle and not always understood, even by those who ought to understand it. In “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” an essay written by Eugene Wigner, a famous physicist, Wigner writes that “the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and there is no rational explanation for it.”

Wow! There is no rational explanation for the enormous usefulness of mathematics in the natural sciences?! Perhaps Wigner is missing something. Might a rational explanation be formulated from the fact that mathematics is logic, logic is wisdom, and “By wisdom the Lord laid the earth’s foundations; by understanding he set the heavens in place.” (Proverbs 3:19)

(See also Mario Livio, Is God A Mathematician?)

In this vein, you might also find interesting physicist Sabine Hossenfelder’s video, which marches nicely alongside her delightful book Lost in Math:

What are the axiom systems to which I refer for purposes of this essay? There are several, but the one that occupies most of college mathematics and the one with which the reader is already familiar from K-12 is the Real Number System (RNS). You have studied “properties” of the RNS in K-12 school math textbooks without being told that these “properties” are axioms of the RNS.

The axioms of the RNS fall into three classes: Eight algebraic axioms, four order axioms, and one topological axiom. You are familiar with the algebraic and order axioms of the RNS but probably not with the sole topological axiom, which is the axiom that makes calculus possible.

Sparing you the details of these 13 axioms, the point of all this has been for you to see that the arc of our interest has been from society to science to mathematics to logic.

Logic is the science of correct reasoning. Logic has two major divisions: deduction and induction. Deduction is the science of inference from premises to conclusion, and induction is the art of selecting premises for deduction.

In K-12, there is no course entitled “Logic.” Students first encounter “Intro to Logic” in college. But even though logic does not appear in K-12 expressly denominated as such, the fact that math is logic, and both math and logic are mediated by language, means that all math work is replete through and through with logic and solving math problems, whether pure or applied. That is precisely the reason why math itself in K-12 is so critically important for success in college and in life—and why it is dangerous to America generally, and profoundly damaging to minority children specifically—to degrade mathematics in America.